Sparsification for Efficient Solutions of Linear Systems
Da Ma and Kazem Cheshmi July 25
* Based on paper: "Sparsified Preconditioned Conjugate Gradient Solver on GPUs" by Da Ma, Khalid Ahmad, Kazem Cheshmi, Hari Sundar, and Mary Hall at SC'25
Efficient Solutions for Linear Systems
Solving a linear system, Ax=b, is a fundamental task in numerous applications where A is a square matrix, x is an unknown vector, and b is a known vector. This computation often consumes the majority of simulation time. Broadly, there are two general approaches to solving such systems: direct methods and iterative methods.
Direct methods decompose the problem into easier-to-solve linear systems, such as triangular systems which can be solved with forward/backward substitution algorithms. While accurate, these approaches typically demand significant memory to store the decomposed systems and can be computationally expensive due to their cubic complexity.
Iterative Methods and Preconditioning
Iterative methods begin with an initial guess and progressively refine the solution in the solve phase until a predefined accuracy is achieved. Each iteration of the solve phase in these solvers often performs a projection. Depending on the computations involved in each iteration, these methods offer a compromise between memory usage and computational cost. Some iterative methods primarily rely on matrix-vector multiplications in their solve phase, while others depend on more complex computations like triangular solvers. The latter category, called a preconditioner-based solver, computes a triangular system as a preconditioner before the solve phase.
A preconditioner-based solver, Preconditioned Conjugate Gradient (PCG), pseudo-code is illustrated in Figure 1. The highlighted lines show where the preconditioner (triangular systems) is computed and later applied in the solve phase. This preconditioning accelerates convergence but incurs the cost of storing the triangular factor and introduces dependencies in its solution. Applying and computing the preconditioner often becomes a bottleneck because the inherent dependencies between iterations limit the effective utilization of parallel resources, especially on GPUs.
One common preconditioning approach to decomposing the input matrix into triangular systems is to use its lower and upper parts. Solving these two triangular systems provides an estimate for the solution of the linear system, while also ensuring that the memory usage of the preconditioner stays within the bounds of the input matrix. To better exploit parallel resources, our goal is to exploit possible parallelism despite the dependencies that exist between iterations.
Figure 2: An example sparse lower triangular matrix.
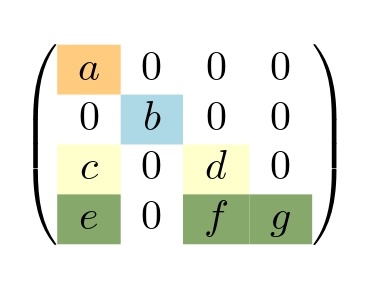
We use a simple lower triangular matrix, shown in Figure 2, to illustrate the impact of these dependencies on parallelism. To illustrate the dependencies between iterations and their impact on parallelization, we utilize a graph visualization. The iterations of computing and applying the preconditioner (highlighted lines in Figure 1) can be modeled as a directed acyclic graph (DAG), where vertices represent iterations and edges signify dependencies between them. An example of this DAG and potential parallel iterations is shown in Figure 3a. All vertices between two dotted lines form a wavefront, which is composed of independent iterations that can run in parallel. While these iterations run in parallel within each wavefront, synchronization is required between wavefronts. For example, three synchronization barriers are needed for the graph in Figure 3a.
Figure 3:
(a) Wavefront parallelism enables partial parallelism for independent iterations. (b) sparsification reduces synchronization and improve parallel iterations.
Sparsified Conjugate Gradient (SPCG)
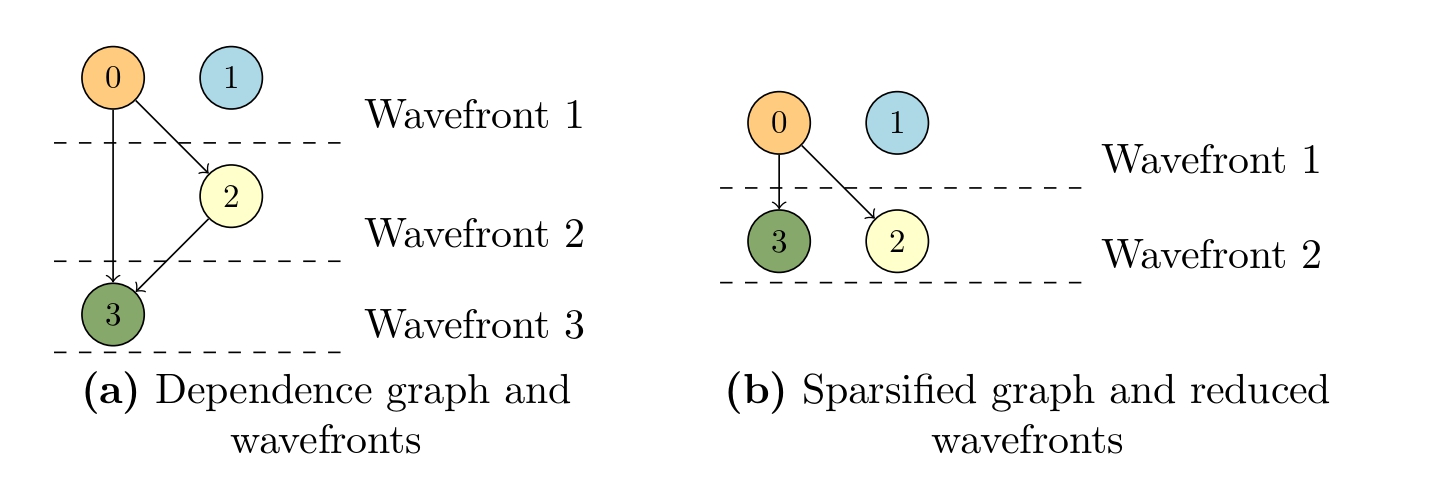
If we can eliminate certain non-zero entries of the preconditioner matrix, the number of wavefronts can be reduced, leading to increased parallelism. For example, removing f from the matrix in Figure 2 leads to a reduction in the number of synchronizations from 3 to 2 in the dependence graph of the preconditioner as shown in Figure 3b. However, removing such entries might cause convergence issues, even as it enhances parallelism. If the value of f is sufficiently small, its removal may not significantly affect convergence while still improving parallel execution. This technique is known as sparsification, and the resulting Conjugate Gradient (CG) variant is referred to as Sparsified CG (SPCG).
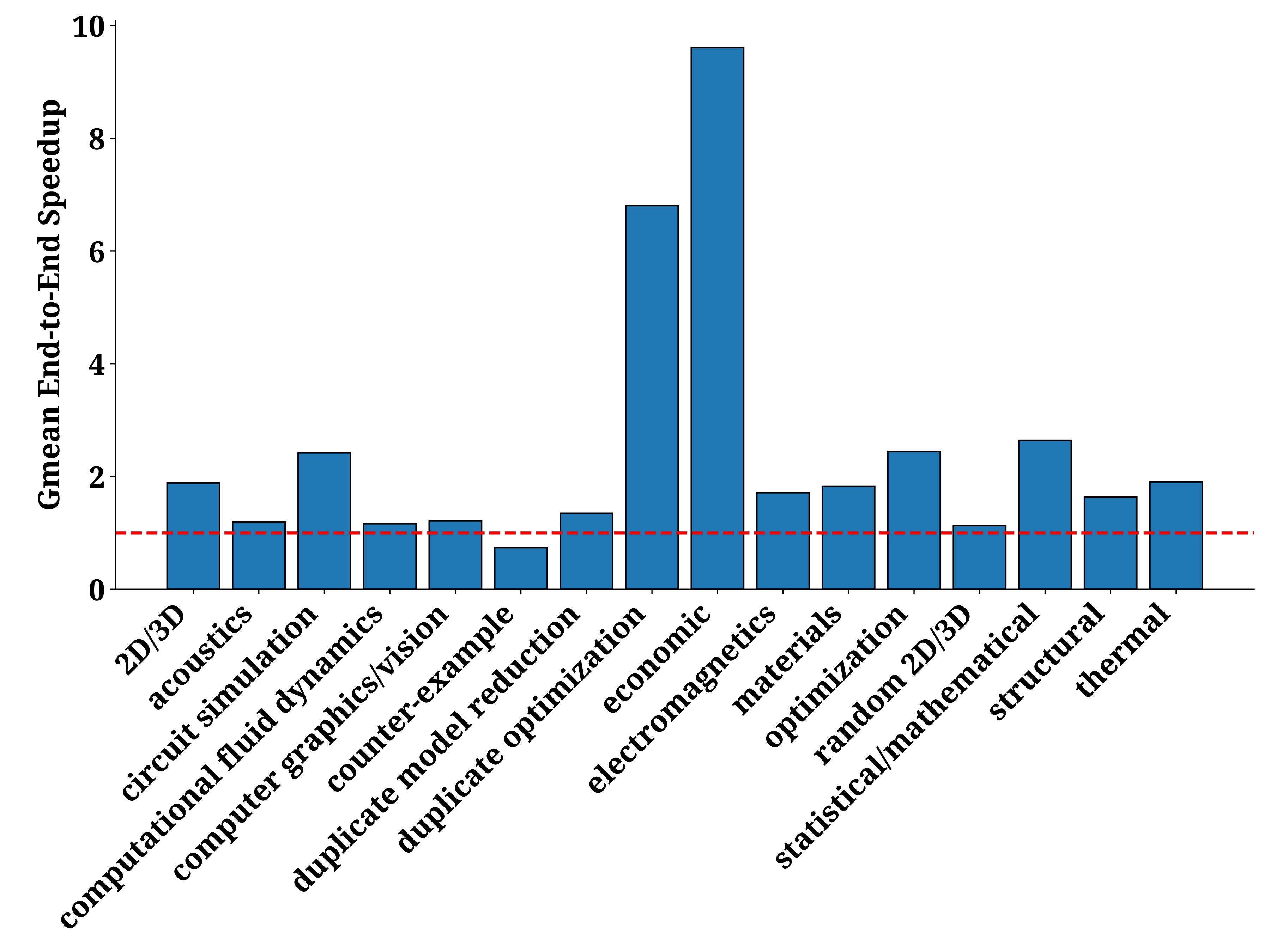
SPCG applies a sparsification algorithm where small values are dropped if they reduce the number of wavefronts. An Incomplete LU factorization with zero fill-in (ILU0) preconditioner is then applied to the sparsified matrix. The resulting triangular systems after sparsification are smaller with fewer wavefronts, significantly improving the end-to-end performance of the linear solver by up to 4.66 times, with a geometric mean of 1.23 times. Figure 4 illustrates the performance of SPCG across various applications. As shown, the speedup varies across different domains, but SPCG generally performs well, with only a few counter-examples showing limited benefits. Conversely, economic modeling, duplicate-optimization, and circuit-simulation workloads show some of the most dramatic speedups, consistently delivering large end-to-end gains.
Figure 4: SPCG-ILU(0) speedup over PCG across applications.
For more detailed information about SPCG, please refer to the SPCG paper, a collaborative work by Da Ma, Khalid Ahmad, Kazem Cheshmi, Hari Sundar, and Mary Hall, researchers from McMaster University and the University of Utah.
