Why should we redefine regularity in sparse computation?

Kazem Cheshmi, Nov 22

Sparse matrix computations are essential in several machine learning and scientific applications. Most elements in a sparse matrix are zero, so the matrix is stored in compressed form to skip computations on zeros. The compression makes sparse methods irregular, challenging efficient use of a processor's memory subsystem. In this post, I explain why a new definition of regularity is needed to improve the performance of sparse codes.

What does regularity mean?

A common approach to accelerate a sparse method is to break it into small “regular” computations, i.e., computations that can use machine resources efficiently. Let’s use the example shown in Figure 1 to explain the current definition of regularity and its pitfalls. The matrix in Figure 1 illustrates a sparse matrix, where rectangular blocks are dense submatrices containing nonzero elements. How would you find regularity in the shown matrix? Probably, most people see each rectangle as a regular region. Not surprisingly, practitioners and researchers typically use the same technique. They find dense submatrices in the sparse matrix and then use efficient dense matrix routines, e.g., a BLAS implementation, to perform the computation. However, this is not the most efficient implementation because it neglects the contiguous storage of nonzero elements in a compressed matrix format. Let’s see how regular regions should be re-defined for sparse code with an example.

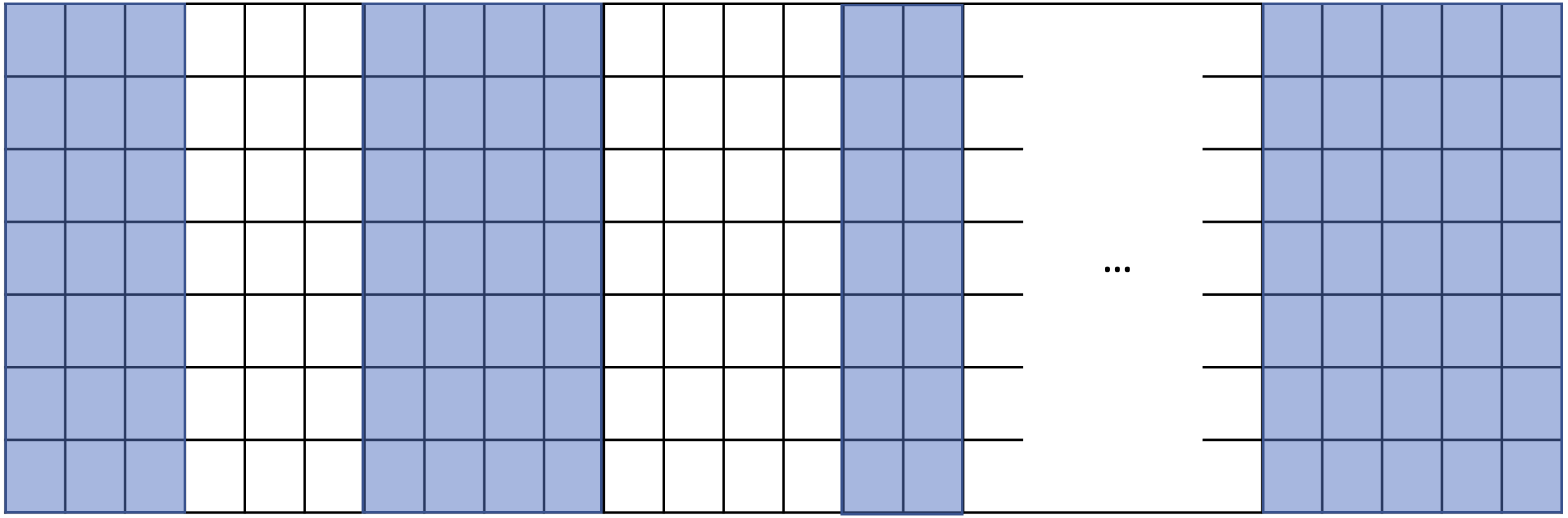
Figure 1 - a sparse matrix composed of several dense submatrices represented with blue rectangles.

Why should we redefine regularity?

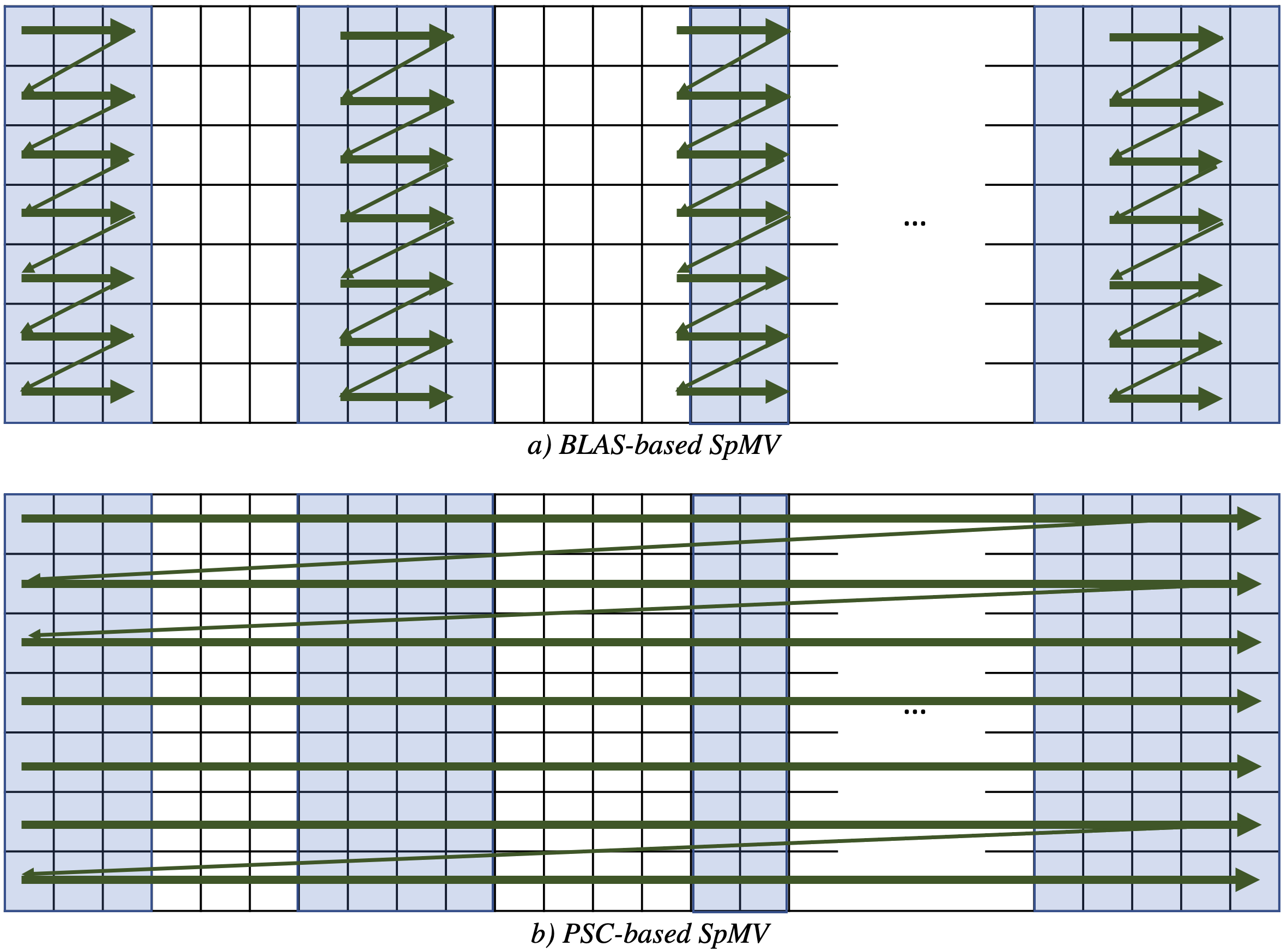
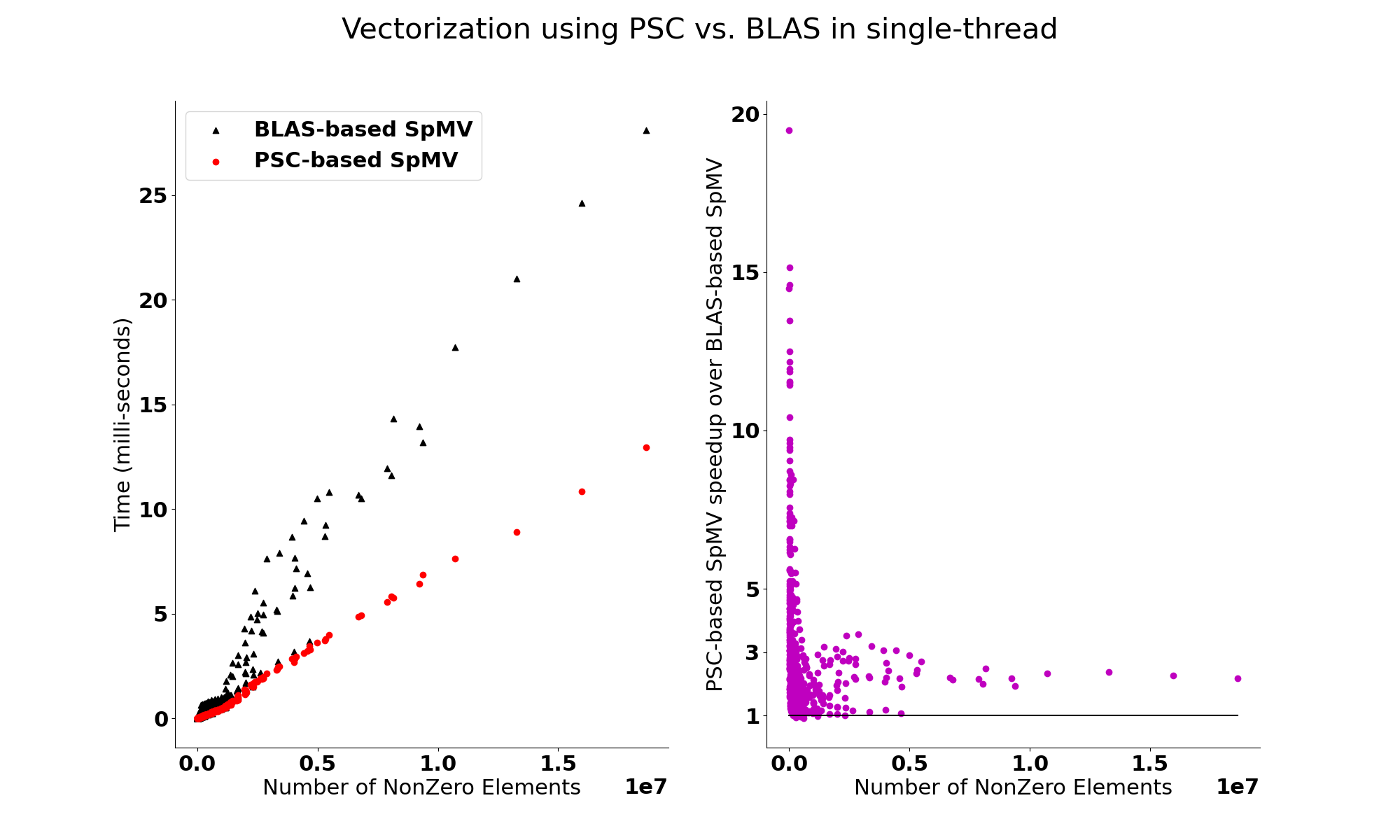
Compressed storage formats in sparse code lead to random accesses. Removing random accesses in dense matrices is often possible by building new schedules and/or code rewriting. This makes prior definitions of regular codes, such as BLAS, heavily rely on strided accesses. But avoiding random accesses in sparse codes is impossible or leads to inefficient execution. There is room for performance optimization even with some random accesses, which demands a new definition of regularity. This new definition is called partially strided codelets . Partially strided codelets can express any regularity in a computation region and provide a qualitative and quantitative measure to apply performance optimization techniques to sparse methods. For example, if a computational region can not be expressed with a PSC, there is no performance benefit in vectorizing it with the given storage. Since sparse methods are memory-bound, PSCs are vital to exploit the memory sub-system in current architectures. 


							 for (int i = 0; i < m; ++i)
							 	for (int j = Ap[i]; j < Ap[i+1]; ++j) 
							 		y[i] += Ax[j] * x[Ai[j]];
Listing 1 - The code sparse matrix-vector multplication.
To illustrate the PSC definition, we compare a PSC-based and a BLAS-based implementation of matrix multiplication for a set of randomly generated matrices with a sparsity pattern shown in Figure 1. Listing 1 shows a sparse matrix-vector (SpMV) multiplication method that computes vector y by multiplying sparse matrix A with x, where A is saved in a compressed sparse row (CSR). The CSR format stores nonzero values row by row in an array (Axi) and uses separate arrays to store column indices (Ai) and row pointers (Ap). We use two SpMV implementations as shown in Figure 2: 1- BLAS-based: goes over blocks and uses a dense matrix-vector multiplication (GEMV) to compute the partial result for y (3a) and 2- PSC-based: visits a row panel as one regular block and goes over them row by row (3b). The random pattern is generated with several dense submatrices, ranging from 64-8K. The size of each submatrix is randomly chosen between 4x8 to 64x70.
Figure 2- Computation schedule for PSC-based and BLAS-based implementations.
The performance of BLAS-based and PSC-based implementations is demonstrated in Figure 3 for a single thread of a cascade processor. As shown, the PSC-based implementation is almost always faster than the BLAS-based. The main reason is that PSCs prioritize contiguously (strided) accesses to Ax, and tolerate random accesses to x. BLAS treats access to Ax and x similarly and thus makes non-contiguous accesses to Ax, degrading spatial locality. The BLAS implementation is known to be fast for large dense matrices, so, we tested for small and large dense sub-matrices for fairness. The code for the experiment is publicly available from here here. There are two more PSC-based implementations and scalarized code in the code base. We show the most performant PSC implementation here, but other PSC implementations are steadily faster than BLAS-based and scalarized SpMV.
Figure 3- The performance PSC-based SpMV versus a BLAS-based SpMV.

What are PSCs?

We model accesses within a computation region with access functions. An access function maps an iteration space to a data space. When there is at least one strided access function and one random (unstrided) access function, the region is defined as a PSC. If all access functions are strided, then it is a fully strided region, e.g. a BLAS call. Finding PSCs can be done at compile-time or runtime. For example, the SpMV code shown in Listing 1 is a PSC. However, for efficiency, we should use sparsity information to extract smaller and more performant PSCs. We have used a differentiation-based PSC synthesis along with a graph-covering problem to find PSCs in SpMV, sparse triangular solver, and sparse-dense matrix multiplication. Please check our paper and code repository for more details.